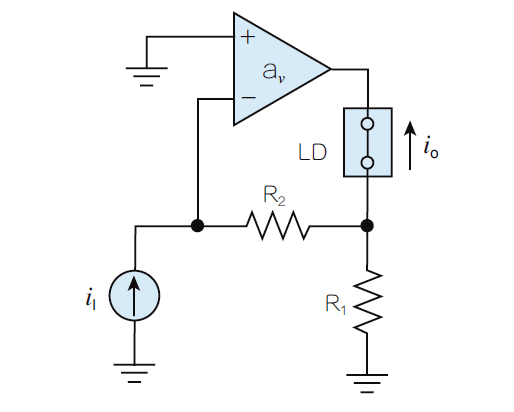
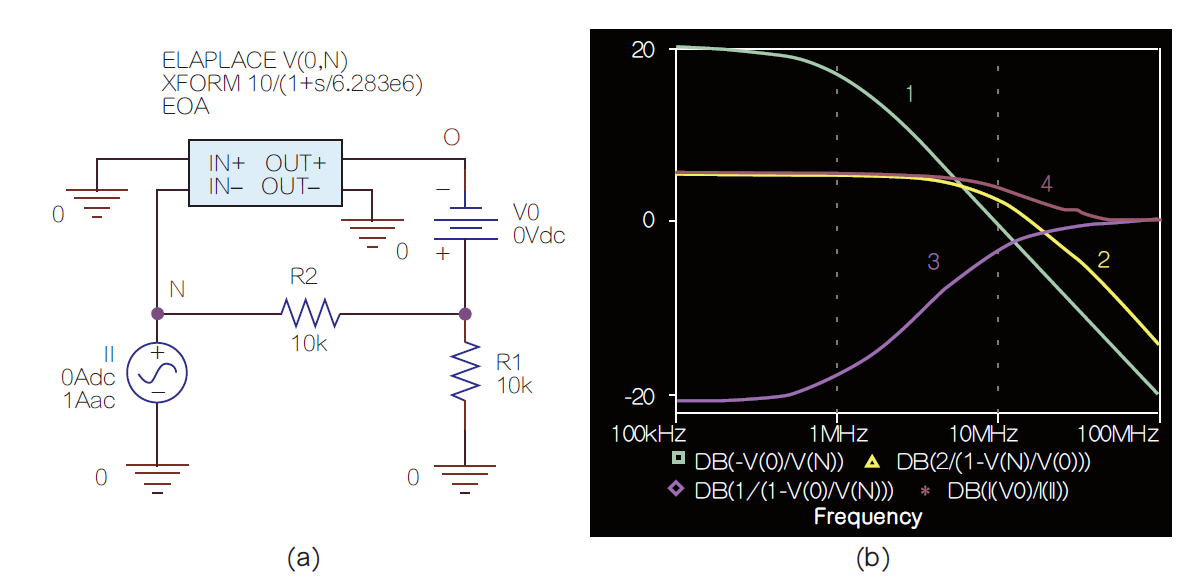
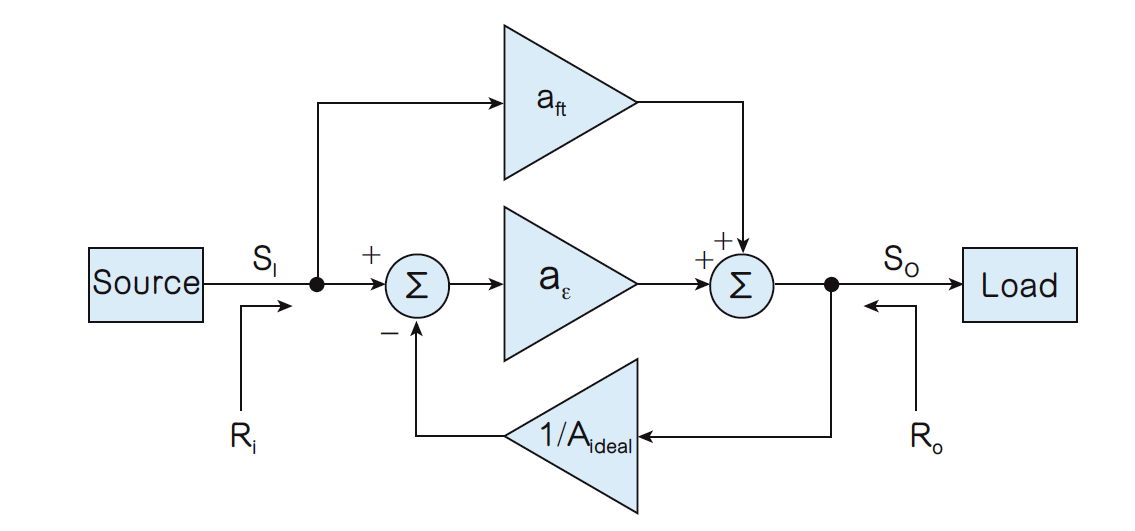
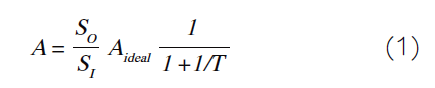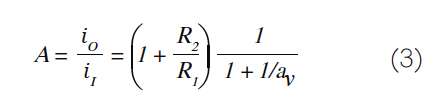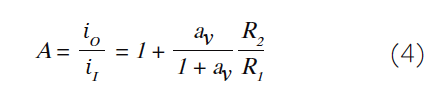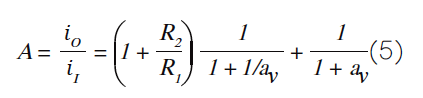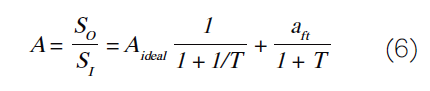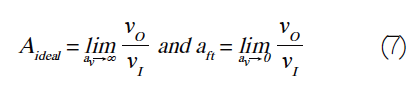图5:考虑误差放大器的馈通并概括图1的电路图。我们应该担心馈通吗?将馈通项a ft s I视为一种杂讯形式是有益的,我们将之反映到误差放大器的输入,即(a ft s I )/a ε。图6可以很容易证明这一点。

显然只要|a ft |<<|a ε |,馈通可能就不会是问题;但是,a ε随着频率滚降(rolls off),a ft变得越来越相关,终占据主导。
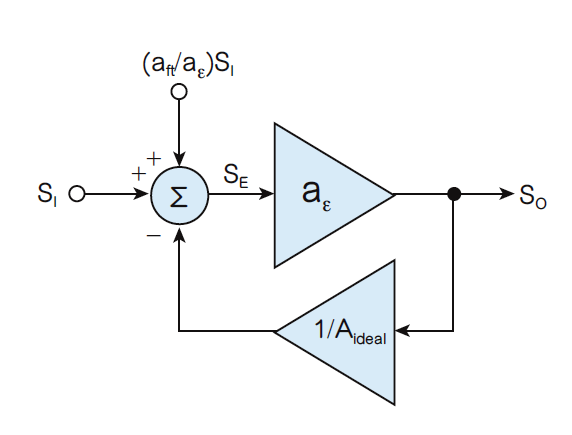
图6:将馈通建模为一种输入杂讯形式。我们是否应关心馈通,取决于实际应用。

图7:使用GBP=1MHz和r o =100Ω的运算放大器来实现积分器。在积分器(integrator)电路中,馈通可能是一个问题。图7使用了一个1MHz运算放大器,其输出阻抗r o=100Ω,以接近理想的传递函数:
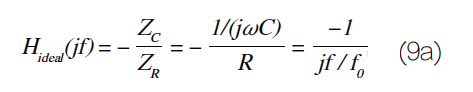
其中f 0是积分器的单位增益频率:
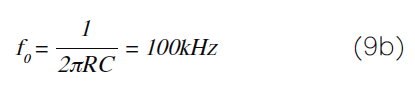
在f→∞时,传递函数应降至零。然而,r o ≠0的存在导致高频馈通增益a ft (∞)≠0。因为在高频时C表现为短路,我们有:
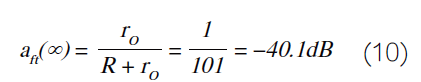
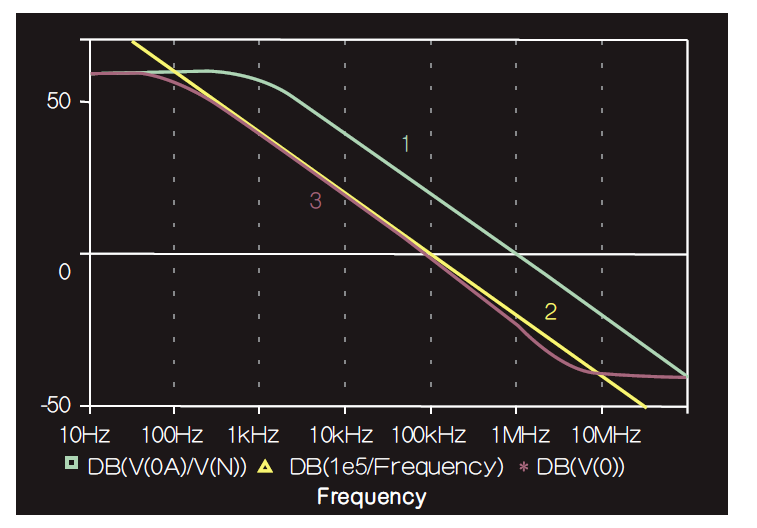
图8:图7积分器的频率特性曲线,迹线#1是开回路增益,迹线#2是理想的积分传递函数H ideal,迹线#3是实际传递函数H(jf)。图8显示实际回应H仅在100H<f<1MHz的范围内接近H ideal。低于100Hz时,C表现为开路,使运算放大器工作在开回路模式。在1MHz时,差异函数D(jf)出现,导入了新的极点频率;这使得下降速率加倍,到3MHz左右,馈通出现。如果想让H更接近H ideal,请使用具有更高GBP的运算放大器。如果馈通在你的应用中是一个问题,可以透过使用具有较低r o的运算放大器或提高R的值来降低a ft(∞)的值(同时降低C的值以保持相同的积分器单位增益频率)。从图9a可以看出,串联输入运算放大器配置中的馈通往往不那么严重,因为输入电压V i必须透过运算放大器输入阻抗z i传输,这个阻抗通常很大。需要注意的是,在高频时z i往往是电容性(capacitive)的,因此会增加馈通量。并联输入配置中的馈通更严重,因为输入电流I I直接馈入回馈网路。但要注意,z o可能会在高频下表现出电感性(inductive behavior),因此其分流减少将允许更多的馈通。对于电流回馈运算放大器(见图9b),输入侧的情况相反。输入接脚上缓冲器的输出阻抗z n通常较小,因此V i透过z n直接馈入回馈网路,而I I则被z n分流到输入缓冲器。
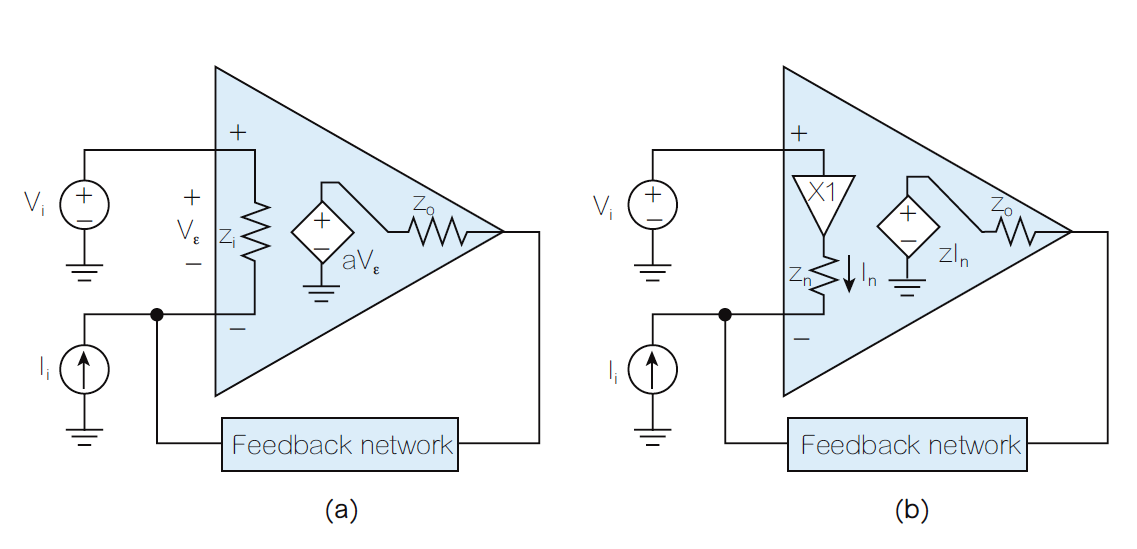
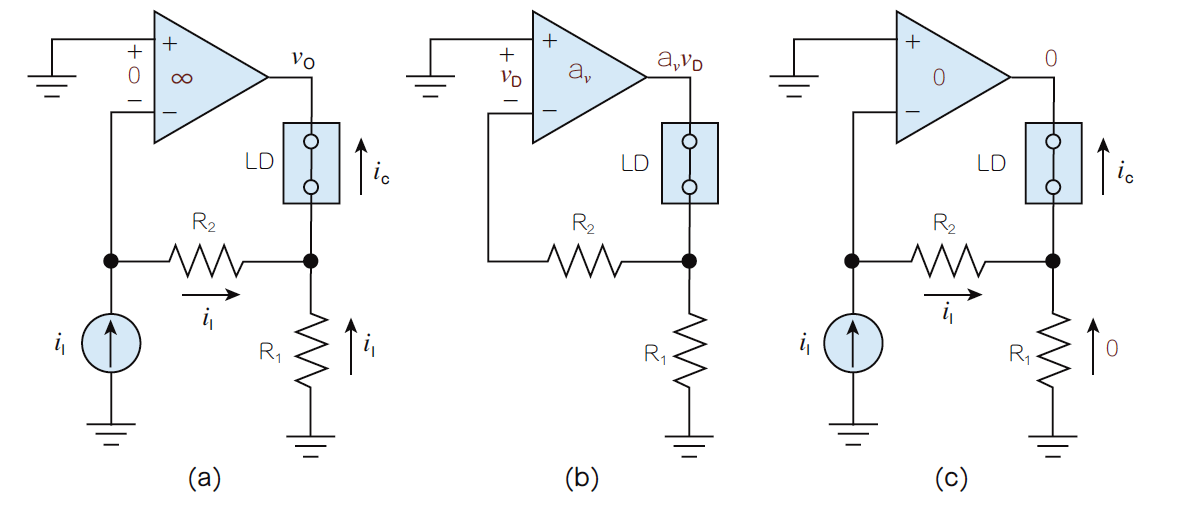
图9:(a)电压回馈;(b)电流回馈运算放大器中的馈通。附录:电流放大器的直接分析我们看一下如何得到图2中电流放大器闭回路电流增益A和输入/输出电阻R i和R o的运算式。该电路非常简单,我们可以直接对其进行分析,忽视回馈分析的必要步骤。要得到A,使用图10a的电路,得到:
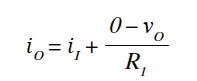
其中: 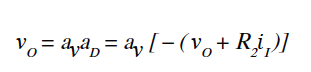
消除v O,整理得到: 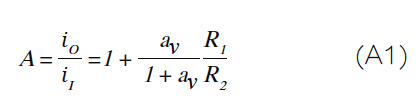
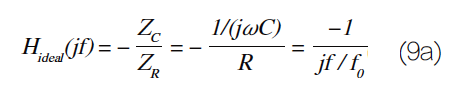
图10:此电路可以得到(a)电流增益A=i O /i I;(b)输入;(c)图2中电流放大器的输出电阻R i和R o。我们也一并找出闭回路终端电阻R i和R o。为了找到输入源i I所见的电阻R i,利用如图10b中的测试电流i,得到v:
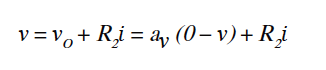
求解比值R i =v/i,得到:

为了找到负载LD所见的输出电阻R o,施加一个测试电压v,如图10c所示,可以得到i: 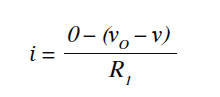
其中: 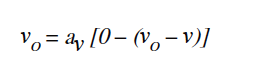
求解比值R o =v/i,得到:

小测验有四个学生(A、B、C和X)正在讨论图11的VI转换器,该转换器使用的运算放大器具有无限大输入电阻、零输出电阻,以及很大的开回路增益a v。具体而言,他们试图找出负载LD所见的输出电阻R o。
图11:(a)VI转换器的理想值i O =(1/R)V i;以及(b)负载所见的电阻R o。A:很明显,LD往上看到运算放大器的输出电阻,假设为零;向下只看到R,因为没有电流流入反相输入端。因此,R o =0+R=R。X:没错!B:错!透过回馈作用,运算放大器在R和源V i之间建立虚拟短路,这被认为是理想的,因此R o=0+0=0。X:正确!C:我听说R o应该比较大...X:这就是我一直说的:R o →∞,至少理想情况下是这样。问题:你觉得上面哪一个学生是对的?